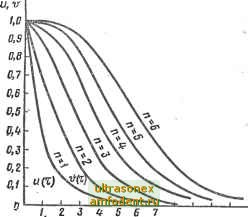в 3 W II tzt

Рис. 4.8

НИЯ и возрастает перерегулирование. РеальиьШ переходный процесс может иметь значительно лучшее качество. Запишем смещенное характеристическое уравнение:

Во Z + Bi z - Ч-... + В 1 г + В - О, (4.22)

б.. =./ - е- лг.. (4.23)

В (4.22) часть коэффициентов - комплексные числа.

Так как фиктивная система находится на границе устойчивости, то (4.22) имеет пару сопряженных мнимых корней Si i:/Pt = ±/и,-.

Если в (4.22) подставить / вместо z И разделить смещенный характеристический полином на мнимую и действительную части, то их можно поочередно приравнять нулю, получив при этом систему двух уравнений

и (фм, щ) = 0; и (фм, (Oi) ~ 0.

Исключив из этой системы со получим искомое значение фм и ц = tgфw [11].

Эту задачу можно решать, используя свойства корней алгебраических уравнений по формулам Виета.

Впервые анализ распределения корней в области устойчивости на примере САУ третьего порядка выполнил И. А. Выш-неградский.

Оценка прямых показателей качества переходного процесса - времени регулирования tp и перерегулирования а (см. § 4.3) - по известным л], I и ц для любого распределения корней и любых начальных условий пока не найдена. Но для определенных классов распределения корней и начальных условий можно построить две кривые: мажоранту и миноранту, которые ограничивают кривую переходного процесса сверху и снизу:

u{t)x{t)v{l), (4.24)

где и (t) - миноранта, а v (t) - мажоранта.

Методы построения мажорант и минорант разработаны С. А. Чаплыгиным, Н. Н. Лузиным, А. А. Фельдбаумом [И] и уточнены А. М. Рубинчиком [8].

Приведем некоторые формулы для расчета мажорант и минорант без доказательства. Для случая вещественных корней и нулевых начальных условий х (0) = О, л: (0) = ... =

х<п-1} (0) = О мажоранта и миноранта описываются соответственно уравнениями

1 +nt + ...

(4.25) (4.26)

(п-1)!

ы(0 = е-1.

-Перерегулирование для этого класса корней отсутствует. На рис. 4.8 показаны кривые и (х) и v (х) для разных степеней уравнения, причем х = tit - относительное время. Чем Bbmie п, тем грубее оценка. Если

учесть величину , то можно сблизить миноранту и мажоранту [2, П1.

Для систем, имеющих среди корней пару комплексно-сопряженных, при тех же начальных условиях мажоранта описывается уравнением (4.25), а миноранта

u{t) = ~v (t). (4.27)

При этом перерегулирование

oe-/t. (4.28)

Если X {0)=Хо, то oXf,e~ * что проиллюстрировано на рис. 4.9.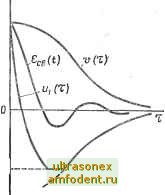

Используя мажоранту и миноранту, можно оценить время регулирования переходного процесса:

где - время регулирования по миноранте; t - время регулирования по мажоранте.

§ 4.6. Корневые годографы

Траектории, описываемые на комплексной плоскости корнями характеристического уравнения замкнутой системы при плавном изменении одного из ее параметров от О до оо, называют корневым годографом. Располагая корневым годографом, можно выбрать необходимое значение варьируемого параметра, соответствующее наиболее выгодному расположению корней с точки зрения требований к качеству конкретной системы. В СССР основополагающими работами в этом направлении были работы К. Ф. Теодорчика, развитые Г. А. Бендрико-вым и С. П. Стрелковым в 1948-1949 гг., в США - работы В. Ивенса в 1950 г.

Используя метод корневого годографа, можно решать следующие задачи [91: построение годографов полюсов передаточной функции замкнутой системы при изменении одного из ее параметров; оценки влияния параметров системы, появляющихся при ее усложнении; качественной и количественной оценки реакции системы на типовой сигнал при изменении значения параметра системы; синтеза корректирующих элементов системы.

Для непрерывных линейных систем существует несколько методов построения корневых годографов, в частности методы Ивенса, Теодорчика-Бендрикова и Удермана. Наиболее трудоемким является метод Ивенса. Используя этот метод, можно оценить несколько вариантов с точностью 3-5 %, что удобцо на первом этапе проектирования. Метод Теодорчика-Бендрикова позволяет проводить более детальные расчеты с использованием ЭВМ.

Рассмотрим метод Ивенса. Передаточная функция замкнутой системы (рис. 4.10)

Wg., (s) = Wl {s)/n + Wy is) W, (s)], (4.29)

где Wy is) W (s) = W (s) (4.30)

- передаточная функция разомкнутой системы.