и кривой D-разбиения заштрихованные и незаштрихованные стороны прямой и кривой были направлены друг к другу (рис. 3.26, а, б). В тех, сравнительно редких, случаях, когда особая прямая имеет место при некопюром конечном значении частоты ы = Ф О и при этом А проходит через нуль и меняет знак, особая прямая штрихуется по приведенному выше правилу, но двойной штриховкой (рис. 3.26, в). Если оке особая прямая имеет место при (а = тФ и при этом А, проходя через нуль, не меняет знака, то особая прямая не штрихуется и исключается из рассмотрения (рис. 3.26, г).

Следует обратить внимание на то, что знак определителя А, определяемого (3.90), зависит от порядка расположения членов в (3.86) и (3.87). Чтобы не допустить грубых ошибок при нанесении штриховки, необходимо в (3.86) и (3.87) сначала написать члены, содержащие параметр, откладываемый по оси абсцисс, т. е. v, а затем члены, содержащие параметр, откладываемый по оси ординат, т. е.

После нанесения штриховки определяют область, претендующую на область устойчивости, т. е. область, внутрь которой направлена штриховка. Затем, выбирая любые значения v == = Vo и [х = Ло, лежащие в этой области, и подставляя их в характеристическое уравнение, нужно с помощью любого из рассмотренных ранее критериев устойчивости определить, все ли корни характеристического уравнения будут при этом левыми. Если при этом не все корни будут левыми, то в плоско-

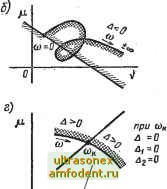Рис. 3.26

сти параметров v и ц области устойчивости нет, т. е. изменением только V и (Л сделат! систему устойчивой нельзя. Если же при этом все корни окажутся левыми, то рассматриваемая область действительно является областью устойчивости D (0). После этого можно разметить области D (т) в любой другой точке плоскости параметров v и [х, имея в виду, что пересечение границы D-разбиения (или особой прямой с двойной штриховкой) из заштрихованной зоны в незаштрихованную соответствует переходу двух комплексно-сопряженных корней из левой полуплоскости корней в правую и наоборот. Пересечение особой прямой с одной штриховкой соответствует переходу одного корня.

Пример 3.7. Пусть характеристическое уравнение замкнутой системы автоматического управления

D(s) = (1 -f Ts)( I + Ts)( 1 -f Ts) -f iC=0.

где К - коэффициент усиления разомкнутой системы; Ti, Тг, Тз - постоянные времени отдельных динамических звеньев.

Требуется построить границу С-разбиення в плоскости коэффициента усиления разомкнутой системы К.

Запишем характеристическое уравнение в виде D (s) = S (s) --

+ vV (s) = О, где S (s) = (1 -Ь Tis) (1 + Ts) (1 -f Тв); N (s) = 1; v = К. Подставляя в характеристическое уравнение s = /w, получаем выражение для границы D-разбиения:

D (/со) = (1-\-т (1 -Ь/соГг) (1 -Ь/Гз) -ЬК = S (/со) + vN (/со) =0.

откуда

v = /(= -S (/co).W (/со) = -(1 -f/соГ!) (1 -f/соГи) (1 -f/соГз) = =X(co)+/K(( ).

Л ( ) = (Г, гн-Г, + тз) - J;

к (ft)) = со [Ti 7-3 со -(7-1 + -f-Ts)].

Задаваясь различными значениями частоты со > О, определяем X (со) н К (со) и строим на комплексной плоскости кривую D-разбиения, соответствующую положительным частотам (сплошная линия на рис. 3.27). Ветвь кривой D-разбиения, соответствующую отрицательным частотам са < О, находим как зеркальное отображение относительной вещественной оси построенного участка для со > О (пунктирная линия на рис. 3.27). Затем кривую D-разбиения штрихуем слева по обходу при изменении частоты со,от -оо до оо.

Кривая D-разбиення делнт плоскость на три области: /, II и /. Претендентом на область устойчивости является область /, так как к ней направлена штриховка. Чтобы проверить, действительно ли эта область является областью устойчивости, задаемся значением v = vo = О, лежащим в этой области, подставляем его в характернсти-

ческое уравнение и определяем корни получающегося при этом характеристического уравие-ння D (s) = (1 + Tys)X X (1 -Ь T,s) (1 + rgs) = = О, все корнн которого Sy= - \/Ti, s=-\/T н s3 = -l/7з являются левыми; следовательно, область / является областью устойчивости D(0).

Так как коэффициент усиления К не является комплексной величиной, то нас будет интересовать только отрезок устойчивости АБ, совпадающий с действительной осью, находящейся в области устойчивости.

Система будет устойчива, если значение К изменяется в пределах -1 < К < Ккр- Отрицательным значениям К соответствует положительная обратная связь. Для нахождения Кр следует определить сначала значение со, при котором Y (и) = 0. Если корень этого уравнения О) = а>в, то Ккр = X (соо). Производя вычисления, получаем

= (71 +72+ 7 з)/(71 72 73); Якр = X ( ) = (1 -Ь-Г2 +Тз) (1 -ЬI/T2 +1 /Тз) -1.

где Та = Гг/7,; т3 = 7з/7,.

На рис. 3.27 показаны области D (0), D (1) и D (2). Область D{3) в данном случае отсутствует. Это означает, что прн положительных значениях Ту, и ТдИ любом значении К невозможно, чтобы все три корня характеристического уравнения одновременно были правыми.

Пример 3,8. Рассмотрим теперь ту же систему, но будем интересоваться влиянием постоянной времени Ту на устойчивость.

Запишем характеристическое уравнение в виде

D(s) = [(\ + Ts){l+TsS)+K] + T,ls{l+Ts)0+ns)] = = S(s)-hv7V(s),

где S(s) = {\-{-T,s)(l-\-TsS)+K; N {s)=s(\+Ts) {l+Tss);

v = T,.

Подставляя в характеристическое уравнение s = /о, получаем выражение для границы D-разбиення:

D (/со) =S (/co)+vA (/со) = (1 -f/cor) (1 +/ю7з) -f +К + Ту /со (1 Ч-/соГг) (l-b/ю7з) = О,

откуда

v = 7i= -[(1 +/С0Г2) (1 -}-/соГз) + К1/[/со (1-f/соП) (1-Ь/а)Гз)1 = --=Х( )-Ь/К (со).